今天来谈谈一个简单而基础的数据结构——二叉树。二叉树相对于普通树结构，其每个结点最多只能有两个子结点。在二叉树中，最重要的操作莫过于遍历。于是下面几个名词就立马来了：前序、中序和后序遍历。

• 前序遍历：先访问根结点，再访问左子结点，最后访问右子结点；
• 中序遍历：先访问左子结点，再访问根结点，最后访问右子结点；
• 后序遍历：先访问左子结点，再访问右子结点，最后访问根节点。

如有一二叉树：

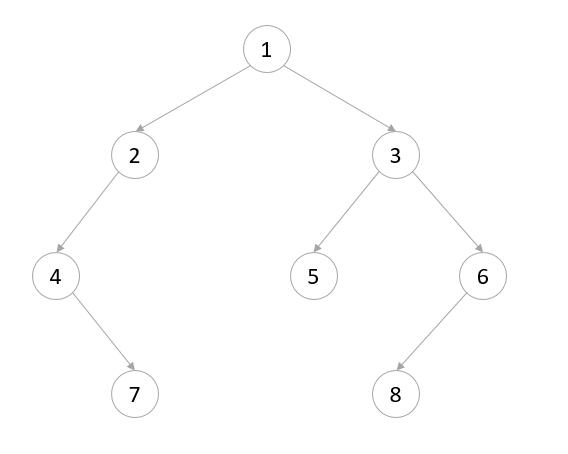
那么其三种遍历结果分别为：

前序遍历：1, 2, 4, 7, 3, 5, 6, 8

中序遍历：4, 7, 2, 1, 5, 3, 8, 6

后序遍历：7, 4, 2, 5, 8, 6, 3, 1

那回到程序中，首先应如何表示这样的二叉树呢？可以这样：

class BinaryTree:

    __slots__ = ('root',)

    def __init__(self, root):
        self.root = root

    def __str__(self, *args, **kwargs):
        return super(BinaryTree, self).__str__(*args, **kwargs)


class Node:

    __slots__ = ('value', 'parent', 'left', 'right')

    def __init__(self, value, parent=None, left=None, right=None):
        self.value = value
        self.parent = parent
        self.left = left
        self.right = right

    def __str__(self):
        return 'Node({})'.format(self.value)

两个类，BinaryTree 和 Node，分别用以代表二叉树以及结点。

BinaryTree 具有一个 root 属性，用于表示根节点。在构造时，当然也是必须传入的。

Node 则有四个属性：

• value：结点的值；
• parent：父结点；
• left：左子结点；
• right：右子结点。

这样就用自己的方式实现了二叉树在 Python 中的表示。

再看三种遍历，基于他们的特点，可以很方便的将其转化为代码实现，分别如下：

def preorder(node):
    """
    结点的前序遍历，生成器函数

    :param node: 遍历的结点，Node 对象
    """

    yield node.value

    for n in [node.left, node.right]:
        if n:
            # require python version >= 3.3
            # equals to:
            # for inner_node in preorder(n):
            #     yield inner_node
            yield from preorder(n)


def inorder(node):
    """
    结点的中序遍历，生成器函数

    :param node: 遍历的结点，Node 对象
    :return:
    """

    if node.left:
        yield from inorder(node.left)
    yield node.value
    if node.right:
        yield from inorder(node.right)


def postorder(node):
    """
    结点的后序遍历，生成器函数

    :param node: 遍历的结点，Node 对象
    :return:
    """

    for n in [node.left, node.right]:
        if n:
            yield from postorder(n)

    yield node.value

很好。不过到这里，又来了一个新的需求：可不可以基于二叉树的前序遍历和中序遍历来反向构造一个二叉树呢？回归两种遍历的特点，前序遍历即是在到达一个结点的时候就立马访问该结点。基于此，那么前序遍历的第一个结点就一定是根结点。而中序遍历则是在访问左子树之后才访问当前结点，因此假设我们在前序遍历中得到了根结点，然后再在中序遍历中找到这个结点。那么根据之前总结的，该结点左边的元素一定在该根节点的左边，该结点右边的元素则一定在该根节点的右边。又回到前序遍历中，前序遍历一定是从左访问到右的，因此在中序遍历定位到的根结点左边所拥有的结点个数（假设是 n），也正好对应了前序遍历中该根结点接下来跟随的 n 个元素。而这 n 个元素又形成了一个子树，从而又可以基于之前的思想再逐层判断。来看一张图：

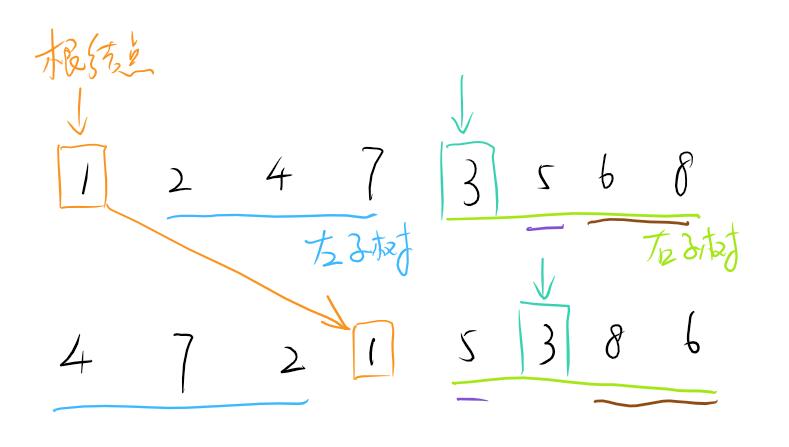
是否理解了呢？基于此，可以以递归的思路实现该逻辑：

def build(preorder, inorder, parent=None):
    """
    根据前序遍历和中序遍历重造树

    :param preorder: 前序遍历列表
    :param inorder: 中序遍历列表
    :param parent: 父节点，Node 对象
    :return: 根节点，Node 对象
    """

    root_node = Node(value=preorder[0], parent=parent)
    index = inorder.index(root_node.value)

    left_nodes, right_nodes = inorder[:index], inorder[index+1:]
    if left_nodes:
        root_node.left = build(preorder[1:len(left_nodes) + 1], left_nodes, root_node)
    if right_nodes:
        root_node.right = build(preorder[len(left_nodes) + 1:], right_nodes, root_node)

    return root_node

最后以之前的例子对代码进行一次验证：

if __name__ == '__main__':
    preorder_traversal = [1, 2, 4, 7, 3, 5, 6, 8]
    inorder_traversal = [4, 7, 2, 1, 5, 3, 8, 6]

    tree = BinaryTree(build(preorder_traversal, inorder_traversal))
    print('PreOrder:', end=' ')
    for value in preorder(tree.root):
        print(value, end=' ')
    print()

    print('InOrder:', end=' ')
    for value in inorder(tree.root):
        print(value, end=' ')
    print()

    print('PostOrder:', end=' ')
    for value in postorder(tree.root):
        print(value, end=' ')

打印的结果如下：

PreOrder: 1 2 4 7 3 5 6 8
InOrder: 4 7 2 1 5 3 8 6
PostOrder: 7 4 2 5 8 6 3 1

最后还有一点可以提一下的是在 BinaryTree 和 Node 两个类中定义了 __slots__。它可以用以限制类中属性的定义。另外在遍历方法中也用到了 Python 一个非常有趣的东西：迭代器。有兴趣可以查阅 Python 官方文档了解更多细节。