跳跃表(Skip Lists)是一种有序的数据结构,它通过在每个节点中维持多个指向其他节点的指针,从而达到快速访问节点的目的。在大部分情况下,跳跃表的效率可以和平衡树相媲美,并且在实现上比平衡树要更为简单,因而得到了广泛的应用。
 如上图所示,是一个跳跃表的示例。由此可以看出跳跃表的几个特点:
如上图所示,是一个跳跃表的示例。由此可以看出跳跃表的几个特点:
- 有序性,如上图中各节点呈递增趋势;
- 跳跃表由多个层组成;
- 跳跃表的第一层始终包含所有元素;
- 如果某个元素位于第 i 层,那该层一下的所有层也会包含此元素。
既然是链表的一种,那在实现时,固然要考虑插入、删除、查找等几个主要方法,下面来一一解析。
查找
要查找一个元素,应从顶层开始,自顶向下查找,又因为其有序性,因此与平衡树上的查找其实很类似。
以之前的图为例,要搜索 12,从顶层为入口,步骤大致如下:
- 从 L3 的第一个节点查询后一个节点 21,发现比 12 大,跳至下一层;
- 从 L2 的第一个节点查询后一个节点 9,比 12 小,因此继续向后;
- 继续查询 L2 的下一个节点 21,比 12 大,跳至下一层;
- 从 L1 的第一个节点开始查询,直至 17 时发现比 12 大,再次调至下一层;
- 从 L0 的第一个节点开始查询,最终发现 12 这个节点,查询结束。
如果要查询的节点在 L0 中都不存在,则应返回并告知“该节点不存在”。
插入
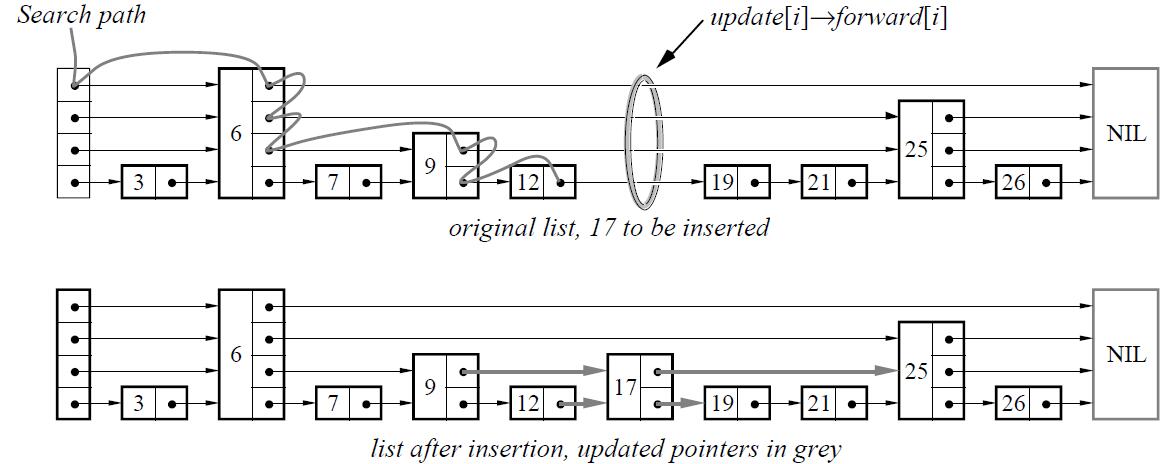
要插入一个节点,不难想象首先需要查询插入的位置,因此首先其实是类似的执行一次查询。然后视情况定是做替换操作还是新增节点。插入的时候要利用一个随机算法来获取该元素要插入的层高,并根据“如果某个元素位于第 i 层,那该层一下的所有层也会包含此元素”这一特性,在要插入层和以下层中都要插入这个新元素。最后还要注意维护层高。以下是插入过程的一个示例:
删除
删除的第一步和插入很类似,首先要执行查找过程。如果查找到,则将该元素删除。这里也必须注意“如果某个元素位于第 i 层,那该层一下的所有层也会包含此元素”这一特性。最后还要注意维护层高。
性能上,跳跃表支持平均 O(log N)、最坏 O(N) 复杂度的节点查找,还可以通过顺序性操作来批量处理节点。
代码实现在网上有很多代码可以参考,且实现方法和细节也不尽相同,因此不在这里提及,而是更多的关注原理。有时候掌握基础与原理其实更为重要。
本文的插图来自于 William Pugh 关于跳跃表的论文《Skip Lists: A Probabilistic Alternative to Balanced Trees》,其中分析了跳跃表的实现及性能,值得研读。

Your Chinese's pretty good and thanks for your article.