在学习排序算法时，我们可以经常看到插入排序的身影。我们继续用扑克牌来描述该算法的实现方式。假设有5张牌以如下方式堆放在桌面上：

将面上的一张牌拿起并放在手上：

因为这是第一张牌，所以我们无需考虑其位置。接着再从桌面上拿起面上的一张牌并与手上的牌进行比较，然后插入到正确的位置上：

接下来的操作与此相同。将梅花5取出然后放在梅花3和梅花8之间：

重复该过程直到所有的牌都从桌上拿起并插入到手中几张牌中的正确位置。

整个过程中，插入排序同时维护两组元素，一组排序后的元素和一组待排序的元素。在上面的扑克牌例子中，桌上的一叠扑克就是待排序的元素组，手上的牌则是排序后的元素组。在程序中处理该算法时，我们将在同一序列结构中处理这两组元素。算法以列表左侧作为排序后的元素位并始终从未排序组中取出第一位进行排序操作。要定位一个元素的正确位置，必须通过搜索来解决，然后移动右边的各元素来为其让位。下面用Python实现一个简单的插入排序算法：

#Sorts a sequence in ascending order using the insertion sort algorithm.
def insertionSort( theSeq ):
    n = len(theSeq)
    # Starts with the first item as the only sorted entry.
    for i in range( 1, n ): 
        # Save the value to be positioned.
        value = theSeq[i]
        # Find the position where value fits in the ordered part of the list.
        pos = i
        while pos > 0 and value < theSeq[pos - 1]:
            # Shift the items to the right during the search.
            theSeq[pos] = theSeq[pos - 1]
            pos -= 1

        # Put the saved value into the open slot.
        theSeq[pos] = value

insertionSort()方法首先假设列表中的第一个元素已经在其正确的位置上。然后从第二位开始迭代并对每一个元素执行排序。由此，排序后的组始终处于列表的前部而待排序的组则处于尾部。循环中的i可以看作这两组的分界点。在内循环中，程序对当前元素进行定位，同时移动列表中的元素以为其腾出位置来。下图演示了一个列表排序的整个过程。

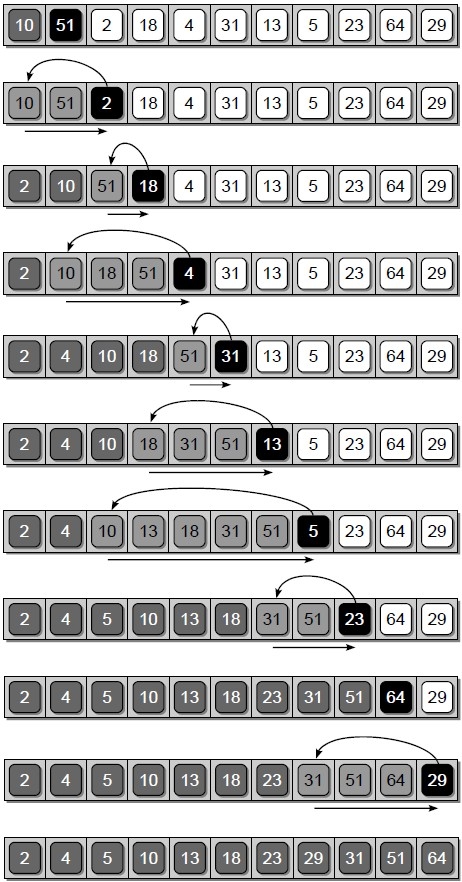
更多请参考：Rance D. Necaise - 《Data Structures and Algorithms Using Python》